如何用队列实现栈?LeetCode第225题
零 题目说明
要求使用2个队列来实现一个后进先出LIFO的栈,该栈支持的方法:入栈push()、出栈pop()、查看栈顶元素top()、栈是否为空empty()。
可以借助队列的方法:入队push()、查看队首元素pop()/peek、查看队列的大小size()、判断队列是否为空isEmpty()。也就是说只能使用单边队列,不能借助DoubleEndedQueue双端队列。
一代码实现思路
定义一个QueueImplementStack<E>类,包含一个成员变量Queue<E> queue,用JDK自带的Queue接口,用链表LinkedList来实例化这个queue;
在构造方法QueueImplementStack()中初始化这个成员变量queue;
入栈push()实现起来比较简单,直接调用LinkedList的add()即可。因为队列的入队操作和栈的入栈操作是一样的,都是添加到后端;
栈是否为空empty()实现也比较简单,直接调用LinkedList的isEmpty()即可。如果链表实现的队列是空的,那么栈也一定为空;
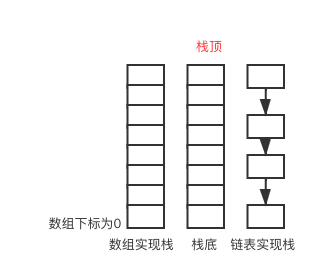
出栈pop()实现起来稍微复杂一点儿,因为栈是LIFO后进先出的,要拿到栈顶元素,其实就是要拿到队尾元素,说白了,就是想要实现从队尾出队就可以了。可是,队列又只能从队首出队,那怎么办呢?如果队列中有n个元素,我们只要想办法先将前面的n-1个元素出队,放另外一个地方暂存,然后队列中只剩下一个元素,就是第n个元素,将其出队,不就实现了出栈嘛。那么,问题又来了,此时队列是空队列了,如果需要继续入栈、出栈操作,岂不是出问题了吗?别急,我们在将队列的前n-1个元素暂存的时候,我们可以新开一个队列assistQueue中,将它们入队到assistQueue,出栈之后,再将原队列的引用指向这个assistQueue不就完美了嘛(#.#)
查看栈顶元素top(),显示一下栈顶元素,并不是真的删除。我们当然可以借助出栈pop()来实现,先调用pop()得到栈顶元素,暂存到临时变量中,然后调用入栈push(),将临时变量重新入栈,最后返回临时变量。这就有点儿像变戏法儿的小把戏一样。好玩儿又有趣。
二 代码实现
import java.util.LinkedList;
import java.util.Queue;
public class QueueImplementStack<E>{
private Queue<E> queue;
public QueueImplementStack(){
queue = new LinkedList<>();
}
//栈是否为空
public boolean empty(){
return queue.isEmpty();
}
//入栈
public void push(E e){
queue.add(e);
}
//出栈
public E pop(){
Queue<E> assistQueue = new LinkedList<>();
while(queue.size()>1){
assistQueue.add(queue.remove());
}
E res = queue.remove();
queue = assistQueue;
return res;
}
//查看栈顶元素
public E top(){
E res = pop();
push(res);
return res;
}
//打印
@Override
public String toString(){
StringBuilder stringBuilder = new StringBuilder();
Queue<E> assistQueue = new LinkedList<>();
assistQueue.addAll(queue);
stringBuilder.append(String.format("QueueImplementStack:size %d\n",assistQueue.size()));
stringBuilder.append("bottom [");
for (int i = assistQueue.size(); i >0; i--) {
stringBuilder.append(assistQueue.remove());
if (i != 1) {
stringBuilder.append(" , ");
}
}
stringBuilder.append("] top");
return stringBuilder.toString();
}
public static void main(String[] args){
QueueImplementStack<Integer> queueImplementStack = new QueueImplementStack();
System.out.println("empty ?" + queueImplementStack.empty());
for (int i = 0; i < 5; i++) {
queueImplementStack.push(i);
}
System.out.println(queueImplementStack);
System.out.println("top():"+queueImplementStack.top());
System.out.println("pop():"+queueImplementStack.pop());
System.out.println(queueImplementStack);
System.out.println("empty ?"+queueImplementStack.empty());
}
}
//结果
empty ?true
QueueImplementStack:size 5
bottom [0 , 1 , 2 , 3 , 4] top
top():4
pop():4
QueueImplementStack:size 4
bottom [0 , 1 , 2 , 3] top
empty ?false三 陷阱小结
在编写toString()方法的过程中,写成了下列代码:
//打印
@Override
public String toString(){
StringBuilder stringBuilder = new StringBuilder();
Queue<E> assistQueue = new LinkedList<>();
assistQueue.addAll(queue);
stringBuilder.append(String.format("QueueImplementStack:size %d\n",assistQueue.size()));
stringBuilder.append("bottom[");
for(int i=0;i<assistQueue.size();i++){
stringBuilder.append(assistQueue.remove());
if(i!=assistQueue.size()-1){
stringBuilder.append(" , ");
}
}
stringBuilder.append("]top");
return stringBuilder.toString();
}打印输出的结果不对,后来经过debug才发现了问题所在。stringBuilder.append(assistQueue.remove());执行之后,队列的长度减小了,不能再次用它作为判断条件了。
的确,这是一个比较有意思的小题目,但是,必须得自己亲自动手敲一遍代码,才能发现更多的问题,才能提升编程能力和算法思维。
四复杂度分析
入栈push():O(1);
出栈pop():O(n);因为每次都要将队列中的n-1个元素搬移到另外一个队列存放,然后再出队第n个元素来实现出栈。
查看栈顶元素top():由于调用了pop(),所以,复杂度也为O(n);
栈判空empty():O(1)。
五 改写查看栈顶元素top()为O(1)
如果我们给类添加1个成员变量,让其始终指向栈顶元素的话,那么,top()的复杂度就是O(1)。可是,具体该怎么实现呢?
public class QueueImplementStack<E>{
private Queue<E> queue;
//添加1个用于存放栈顶元素的成员变量
private E topElement;
public QueueImplementStack(){
queue = new LinkedList<>();
}
//栈是否为空
public boolean empty(){
return queue.isEmpty();
}
//入栈
public void push(E e){
queue.add(e);
//每次入栈时,都把栈顶元素赋值给topElement
topElement = e;
}
//出栈
public E pop(){
Queue<E> assistQueue = new LinkedList<>();
while(queue.size()>1){
//每次出栈前,都要把栈顶元素给topElement。因为不这样操作的话,原栈顶元素出栈之后,topElement就不再指向栈顶元素了
topElement = queue.remove();
//然后把这个topElement放到assistQueue中
assistQueue.add(topElement);
}
//最后,再拿到仅存的那个元素,使之出栈即可
E res = queue.remove();
//将queue重新指向辅助队列
queue = assistQueue;
return res;
}
//查看栈顶元素
public E top(){
return topElement;
}六 队首“充当”栈顶来实现
前面,我们通过队列来实现的栈,相当于队首是栈底,队尾是栈顶。如果我们可以换一个思路,把队列的队首当作栈顶的话,那么出栈和查看栈顶元素,就变得非常简单了:直接调用队列的出队、查看队首元素即可。因为,对本身就是支持队首出队、查看队首元素的。
那么,问题又来了,入栈操作就变得复杂了:队列是先进先出,栈先进后出,该怎么实现呢?于是,我们想到,针对队列queue而言,我们每次入队元素e时,都把队列queue中的已有的所有元素先逐个逐个出队,并入队到另外一个辅助队列assistQueue中去,然后将元素e入队到当前队列queue,最后再将assistQueue中的所有元素出队,并入队到当前队列queue中去,就解决了这个问题。
//队首充当栈顶的实现方式:出栈、查看栈顶元素变得非常简单
//比较不容易处理的是,入栈操作,
public class QueueImplementStack<E>{
private Queue<E> queue;
public QueueImplementStack(){
queue = new LinkedList<>();
}
//栈是否为空
public boolean empty(){
return queue.isEmpty();
}
//入栈
public void push(E e){
//借助1个辅助队列,先将队列所有元素出队到辅助队列
Queue<E> assistQueue = new LinkedList<>();
while (queue.size() > 0) {
assistQueue.add(queue.remove());
}
//元素e入队操作
queue.add(e);
//再将辅助队列中的元素全部出队到当前队列中去,
while (assistQueue.size() > 0) {
queue.add(assistQueue.remove());
}
}
//出栈
public E pop(){
return queue.remove();
}
//查看栈顶元素
public E top(){
return queue.peek();
}
} 一句话总结:这种思路有点儿移花接木,偷梁换柱的感觉。倒是很有意思。