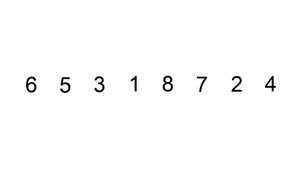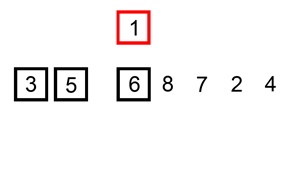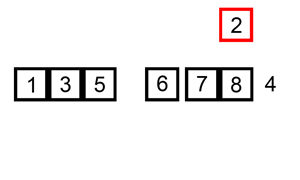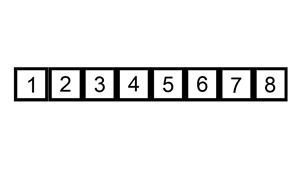
插入排序算法
1定义和说明
见名知意,插入排序算法,就是对于一个给定的数组,假设前n项是已经排好序的,然后看第n+1项,把它插入到前面已经排好序的n项中去,且要求插入之后的n+1项数据,也是排好序的。好比方我们在斗地主的时候,不断抓牌、理牌的过程:我们抓第2张牌的时候,先把它放到第1张的后面,然后判断它是否小于我们手中的第1张牌?如果小于第1张牌,则交换这2张牌的位置,否则(大于或等于第1张牌),它就放在原地(放在第1张牌的后面)。接下来,开始抓第3张牌并放到第3个位置,再比较它和第2张牌的大小,如果大于或等于第2张牌,则放在原地不动,否则交换它和第2张牌的位置。注意:交换之后,要继续比较它和第1张牌的大小,如果它还小于第1张牌,则交换它和第1张牌的位置,否则,它就放在第2的位置。然后,继续抓牌,并重复执行这个过程。当然,我们在真的斗地主的时候,一般没人会这么繁琐的理牌,肯定是抓到牌之后,马上就知道它应该放在的位置,并直接插入到它应该放的位置。但是,计算机在执行插入排序的时候,的的确确就是完全按照上述一步一步执行的。
2实现思路
对于给定的长度为n的数组arr,我们从第i个元素开始,假定[0,i)之间的元素是已经排好序的,第[i,n)区间的元素是无序的,然后判断第i个元素arr[i]是否小于arr[i-1]?如果不小于,则不作交换处理,则数组的[0,i+1)是有序的,[i+1,n)是无序的,然后把第i+1个元素继续按这个思路插入到前面的i个元素中去。如果小于,则交换arr[i]和arr[i-1]的位置;交换之后,继续判断arr[i-1]和arr[i-2]的大小并选择是否需要交换,直到走到数组的第1个元素arr[0]为止。
3代码实现
public class InsertionSort{
//本类是插入排序工具类,没有实例化的需求,所以构造方法私有化
private InsertionSort(){};
//带泛型的选择插入排序算法,
public static <T extends Comparable<T>> void sort(T[] arr){
//从第i个元素开始循环,直到最后1个元素结束,外循环这里的[i,arr.length)区间的元素都是没排序的。
for(int i=0;i<arr.length;i++){
//内循环这里的第[0,j==i)区间的元素是拍好序的
for(int j=i;j>0;j--){
//拿出这第i个元素和前面的已排好序的元素逐一比较,如果小于则交换位置
if(arr[j].compareTo(arr[j-1])<0){
swap(arr,j,j-1);
}else{
//如果不小于即arr[j]>=arr[j-1],则它一定也不小于更前面的元素,直接跳出内循环
break;
}
}
}
}
private static <T> void swap(T[] arr,int i,int j){
T temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
public static void main(String[] args){
Integer[] arr={6,4,2,33,11,5};
InsertionSort.sort(arr);
for(Integer k:arr){
System.out.print(k+" ");
}
}
}
//结果:
//2 4 5 6 11 33 4 对自定义类使用插入排序算法进行排序
我们对插入排序算法已经可以支持泛型的排序算法,即对任意数据类型的数据进行排序。我们自定义一个Student类,让其实现Comparable接口,在compareTo()方法中,先按身高排序,再按年龄进行排序。
public class Student implements Comparable<Student>{
private String name;
private int height;
private int age;
public Student(String name,int height,int age){
this.name=name;
this.height=height;
this.age=age;
}
@Override
public int compareTo(Student stu){
if(this.height!=stu.height){
return this.height-stu.height;
}else{
return this.age-stu.age;
}
}
@Override
public String toString(){
return "Student: name="+name+" height="+height+" age="+age;
}
}在InsertionSort的main方法中,对Student[]数组进行排序,代码片段如下:
public static void main(String[] args){
Student[] students={new Student("Jim",120,7),
new Student("Kate",120,7),
new Student("Tom",110,5)};
SelectionSort.sort(students);
for(Student stu:students){
System.out.println(stu);
}
}
//结果如下:
//Student: name=Tom height=110 age=5
//Student: name=Jim height=120 age=7
//Student: name=Kate height=120 age=7
从上,可以看到,支持泛型的选择排序算法,可以对任意类型的数据进行排序了。同时,看到排序之后,Jim和Kate这2个学生对象的身高,年龄一致,且在原数据中,Jim排在前面,排序之后的结果Jim依然在Kate前面。所以,验证了插入排序是稳定的排序算法。
5 复杂度分析
从插入排序算法的代码看出:
//带泛型的选择插入排序算法,
public static <T extends Comparable<T>> void sort(T[] arr){
//从第i个元素开始循环,直到最后1个元素结束,外循环这里的[i,arr.length)区间的元素都是没排序的。
for(int i=0;i<arr.length;i++){
//内循环这里的第[0,j==i)区间的元素是拍好序的
for(int j=i;j>0;j--){
//拿出这第i个元素和前面的已排好序的元素逐一比较,如果小于则交换位置
if(arr[j].compareTo(arr[j-1])<0){
swap(arr,j,j-1);
}else{
//如果不小于即arr[j]>=arr[j-1],则它一定也不小于更前面的元素,直接跳出内循环
break;
}
}
}
}当外层循环i=0时,内循环执行0次,i=1时,内循环执行1次,i=2时,内循环2次,i=n时,即数组长度时,内循环n次。所以,总循环次数=0+1+2+…+n=n(1+n)/2=1/2(n2+n),则世界复杂度是O(n2)。验证一下这个时间复杂度:
构建两个辅助工具类:
第1个工具类ArrayGenerator:
import java.util.Random;
public class ArrayGenerator {
private ArrayGenerator(){}
//生成长度为n的整型数组,数组元素上限为bound的随机数
public static Integer[] generateRandomArray(int n,int bound) {
Integer[] randomArray = new Integer[n];
Random random = new Random();
for (int i = 0; i < n; i++) {
randomArray[i] = random.nextInt(bound);
}
return randomArray;
}
}构建第2个辅助工具类,SortingHelper
public class SortingHelper {
private SortingHelper() {
}
//传入参数为一个T类型的数组,验证其是否已经排好序的,如果每个元素比它前一个元素都大,则该数组是已经排好序的,返回true
public static <T extends Comparable<T>> boolean isSorted(T[] arr) {
for (int i = 1; i <arr.length; i++) {
if (arr[i-1].compareTo(arr[i]) > 0) {
return false;
}
}
return true;
}
//传入1个排序方法,以及一个待排序数组,根据排序方法的不同,对数组执行不同的排序,并记录该排序耗时,最后验证排序是否正确
public static <T extends Comparable<T>> void sortTest(String sortName,T[] arr){
long beginTime = System.currentTimeMillis();
if (sortName.equals("SelectionSort")) {
SelectionSort.sort(arr);
}
if (sortName.equals("InsertionSort")) {
InsertionSort.sort(arr);
}
long endTime = System.currentTimeMillis();
double time = (endTime - beginTime) / 1000.0;
if (!SortingHelper.isSorted(arr)) {
throw new RuntimeException(sortName+" failed");
}
System.out.println(String.format("%s ,%d ,%s s",sortName,arr.length,time));
}
}
插入排序算法的main()添加下述代码段,进行测试:
public static void main(String[] args){
Student[] students={new Student("Jim",120,7),
new Student("Kate",120,7),
new Student("Tom",110,5)};
SelectionSort.sort(students);
for(Student stu:students){
System.out.println(stu);
}
int[] size = {10000, 100000};
for (int i = 0; i < size.length; i++) {
//调用辅助工具类ArrayGenerator.generateRandomArray()生成2个长度、元素的随机数,分别为1万,10万的数组
Integer[] integers = ArrayGenerator.generateRandomArray(size[i], size[i]);
//调用辅助工具类SortingHelper.sortTest(),分别对这2个数组进行插入排序,并验证排序正确性
SortingHelper.sortTest("InsertionSort", integers);
}
}
//结果:
//Student: name=Tom height=110 age=5
//Student: name=Jim height=120 age=7
//Student: name=Kate height=120 age=7
//InsertionSort ,10000 ,0.226 s
//InsertionSort ,100000 ,24.634 s从上,可以看到,1万个元素的数组插入排序耗时0.226s,而10万个元素的数组插入排序耗时24.634s,耗时差不多是前者的100倍,而数据量是前者的10倍。因此,说明该排序算法时间复杂度是O(n2)。
6 优化插入排序算法
从现有的排序算法分析,
//带泛型的插入排序算法,
public static <T extends Comparable<T>> void sort(T[] arr){
//从第i个元素开始循环,直到最后1个元素结束,外循环这里的[i,arr.length)区间的元素都是没排序的。
for(int i=0;i<arr.length;i++){
//内循环这里的第[0,j==i)区间的元素是拍好序的
for(int j=i;j>0;j--){
//拿出这第i个元素和前面的已排好序的元素逐一比较,如果小于则交换位置
if(arr[j].compareTo(arr[j-1])<0){
swap(arr,j,j-1);
}else{
//如果不小于即arr[j]>=arr[j-1],则它一定也不小于更前面的元素,直接跳出内循环
break;
}
}
}
}当我们执行内层循环,当arr[j]<arr[j-1]的时候,我们就需要交换它俩的位置,此时,如果arr[j-2]依然小于交换之后的arr[j-1]的情况下,我们还得交换一次。同时,如果再次交换之后,前面的元素依然小于交换之后的话,仍然要交换一次。那么,有没有聪明一点儿的做法呢?比如,当我们抓牌、理牌的时候,此时手上的牌分别是3,6,8,9,我们抓了一张5,这时候,按照现有的算法逻辑,先比较5和9,发现小于,就交换位置,交换之后,变成3,6,8,5,9,接着,比较8和5,继续交换,变成3,6,5,8,9,继续比较6和5,并交换位置,最后来到,3,5,6,8,9。这里执行了3次比较和交换的操作。试想,手上的牌分别是3,6,8,9,我们抓了一张5的时候,放在9的后面,5<9,把5抽出来,放在另外一个地方,腾出位置,让9移动到5原来的位置,5<8,让8移动到9原来的位置,进而5<6,让6移动到8原有的位置,最后5不小于3,就把5放到6原有的位置。这样,和原有的算法比较,就减少了3次交换位置的操作,取代的是6,8,9三次顺移赋值的操作。于是,我们可以把算法的实现逻辑,改造成下面的实现:
//带泛型的插入排序算法
public static <T extends Comparable<T>> void sortPlus(T[] arr){
//从抓到的这第i张牌的位置开始,外层循环从[i,arr.length)的元素仍然是未排序的
for(int i=0;i<arr.length;i++){
//把这个第i张牌"拿走",放到一个新的地方temp处存放,
T temp=arr[i];
//另起一个变量,让它等于第张牌的位置开始,从i到i-1,从右到左的顺序,开始循环。把这个变量放在循环外面的原因是,当我们把6,8,9三张已排序的牌,依次顺移之后,如果前面再没有比它大的元素的话,这个变量j正好要放我们拿走的那个第i张牌,即5应该放的位置。且,我们还要再次用到它,如果放到for loop里面的话,离开loop之后,它的作用域就消失了,我们无法用到它
//注意,这里的j其实就是将来我们要把arr[i]插入的位置。
int j;
for(j=i;j>0;j--){
//从"拿走的"这个第i张牌位置开始,从右到左,如果相邻的两张牌,左边的牌<右边的牌,则通过右边的牌=左边的牌的赋值方法,来实现依次顺移的操作
if(temp.compareTo(arr[j-1])<0){
arr[j]=arr[j-1];
}
//********************************************************
//注意:这里的else从句必须带上,否则,该算法可能会报错,比如:传入3,1,5的数组,排序之后的输出结果,变成了5,3,5。
//*******************************************************
else{
break;
}
//对于上述这段for loop代码,也完全可以改造成下述
//for(j=i;j>0 && arr[j].compareTo(temp)<0;j--){
// arr[j]=arr[j-1];
//}
}
//好了,所有小于我们拿走的那个第i张牌,依次顺移走了。此时,j就是我们拿走的那个第i张应该放入的位置,把它放进去就结束这一轮的顺移操作。我们又从第i+1张牌开始,重复此过程。这就省去了逐个交换位置的操作了。
arr[j]=temp;
}
}
在我们工具类的SortingHelper中,增加这个sortPlus()改进版的插入排序算法的分支,并进行测试对比
public static <T extends Comparable<T>> void sortTest(String sortName,T[] arr){
long beginTime = System.currentTimeMillis();
if (sortName.equals("SelectionSort")) {
SelectionSort.sort(arr);
}
if (sortName.equals("InsertionSort")) {
InsertionSort.sort(arr);
}
//加入优化插入排序算法的分支
if (sortName.equals("InsertionSortPlus")) {
InsertionSort.sortPlus(arr);
}
long endTime = System.currentTimeMillis();
double time = (endTime - beginTime) / 1000.0;
if (!SortingHelper.isSorted(arr)) {
throw new RuntimeException(sortName+" failed");
}
System.out.println(String.format("%s ,%d ,%s s",sortName,arr.length,time));
}InsertionSort的main()方法中,执行测试对比:
public static void main(String[] args) {
int[] dataSize = {10000, 100000};
System.out.println("Random array:InsertionSort VS InsertionSortPlus:");
for (int n:dataSize ) {
//开一个长度为1万,元素大小上限也为1万的随机数组
Integer[] arr = ArrayGenerator.generateRandomArray(n, n);
//在排序之前,对这个数组进行复制,便于后面使用不同的方法对相同的数组执行排序测试对比
Integer[] arr2 = Arrays.copyOf(arr, arr.length);
SortingHelper.sortTest("InsertionSort", arr);
SortingHelper.sortTest("InsertionSortPlus",arr2);
}
}
//执行结果:
//Random array:InsertionSort VS SelectionSort:
//InsertionSort ,10000 ,0.247 s
//InsertionSortPlus ,10000 ,0.18 s
//InsertionSort ,100000 ,28.561 s
//InsertionSortPlus ,100000 ,15.916 s从中,我们看到,无论是对于1万还是10万数量级的数组,我们优化后的改进版的插入排序算法的性能都要比之前的好一些。当然,这一点儿改进还不足以吸引人,毕竟还真是相同数量级上的提升。等我们使用一些高级排序算法的时候,比如快速排序算法、合并排序算法,才是更高维度的算法,其性能要远远高于我们现在所使用的的算法。
7 对比选择排序算法和插入排序算法的性能
从上面的分析得出插入排序算法的时间复杂度也是O(n2),即使我们对其进行了改造和优化,其复杂度也依然是保留在O(n2)这个数量级。但是,在实际工程中,和我们之前用到的选择排序算法相比,插入排序算法的性能旺旺要好一些。
例如:给定数组,1,2,4,7,使用选择排序算法的时候,每次都要先假定待排序数据中的第一个是最小元素,然后再从剩下的元素中找一个最小的元素出来,并和认定的那个元素进行比较大小并交换。我们从直观上能看出来,对于这个已经是有序的数组,使用选择排序算法的话,显然做了很多无用功。这样一来,选择排序算法的时间复杂度依然是O(n2)。
而,对于插入排序算法的话,外层循环依然是n次,而对于内层循环,每次都不满足待插入元素的前一个元素比它小,这样就相当于复杂度退化到常数级别的了,进而整体复杂度可以粗略认为是O(n)级别的了。
Wikipedia关于insertion-sort的说明:
- More efficient in practice than most other simple quadratic (i.e., O(n2)) algorithms such as selection sort or bubble sort
- Adaptive, i.e., efficient for data sets that are already substantially sorted: the time complexity is O(kn) when each element in the input is no more than k places away from its sorted position
我们还是实际拿数据来测试对比一下,这次我们用ArrayGenerator辅助工具类来构造有序的数组。
public static Integer[] generateOrderedArray(int n) {
Integer[] orderedArray = new Integer[n];
for (int i = 0; i < orderedArray.length; i++) {
orderedArray[i] = i;
}
return orderedArray;
}main()代码如下:
public static void main(String[] args) {
int[] dataSize = {10000, 100000};
System.out.println("Random array:InsertionSort VS SelectionSort:");
for (int n:dataSize ) {
Integer[] arr = ArrayGenerator.generateRandomArray(n, n);
Integer[] arr2 = Arrays.copyOf(arr, arr.length);
SortingHelper.sortTest("SelectionSort", arr);
SortingHelper.sortTest("InsertionSortPlus",arr2);
}
////
System.out.println("Ordered array:InsertionSort VS SelectionSort:");
for (int n:dataSize ) {
Integer[] arr = ArrayGenerator.generateOrderedArray(n);
Integer[] arr2 = Arrays.copyOf(arr, arr.length);
SortingHelper.sortTest("SelectionSort", arr);
SortingHelper.sortTest("InsertionSort", arr2);
}
}
//输出结果:
Random array:InsertionSort VS SelectionSort:
SelectionSort ,10000 ,0.165 s
InsertionSortPlus ,10000 ,0.24 s
SelectionSort ,100000 ,15.211 s
InsertionSortPlus ,100000 ,17.546 s
Ordered array:InsertionSort VS SelectionSort:
SelectionSort ,10000 ,0.08 s
InsertionSort ,10000 ,0.0 s
SelectionSort ,100000 ,8.293 s
InsertionSort ,100000 ,0.001 s对于元素是随机数的数组而言,选择排序和插入排序性能几乎相当。
但是,当数组元素是部分有序或者接近有序的情况下,数据量大的情况下,插入排序算法的性能要远远胜于选择排序算法。
当然,这种是比较理想的情形,还有就是这种也只是相同数量级的胜出,跟高级排序算法相比,这根本算不了什么。