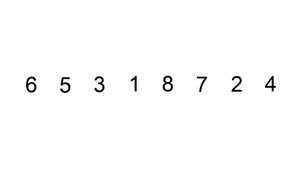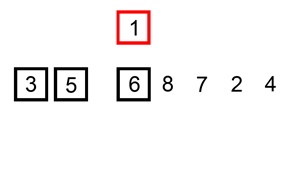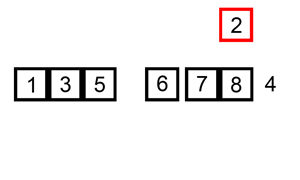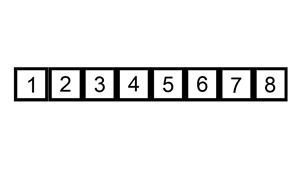选择排序算法
Contents
1 定义和说明
所谓的选择排序算法,就是对于一个给定的数组,首先,选择其中的最小元素放在第一个位置处;然后,从剩下的元素中,再选择其中的最小元素,并把它放到数组的第二个位置处;接下来,重复这一过程,直到最后一个元素,它自己就是剩余元素的最小元素,自然就放到了最后的数组的位置处。
2 实现思路
对于一个给定的数组arr,首先,假定第1个元素是最小的,然后从第2个到最后1个元素中,选择一个最小的元素出来,如果选择出来的这个最小元素比我们假定最小的那个元素(即第1个元素)还要小的话,则交换它们的位置。如果选择出来的这个最小元素不小于我们假定最小的那个元素(即第1个元素)的话,则意味着我们假定最小的那个元素(即第1个元素),的确就是整个数组中最小的元素,所以它就呆在原来的位置处,我们什么也不用做。这样下来,就保证第1个元素一定是整个数组中最小的那个元素。
接下来,我们假定第2个元素是最小的元素,然后从第3个到最后1个元素中,选择1个最小的元素和第2个元素进行比较和交换的过程,处理之后,这第2个元素就一定是整个数组中除第1个元素之外的最小元素。
以此类推,当我们处理完数组的倒数第2个元素之后,就可以不用再走下去了,剩余最后1个元素一定是整个数组中剩余元素中的最小那个元素,因为就剩下它自己了,没得比了,同时,它也一定是整个数组中最大的那个元素了,所以,它就呆在数组的最后位置处。
3 代码实现
import java.util.Random;
public class SelectionSort{
//私有化构造方法
private SelectionSort(){};
//选择排序方法
public static void sort(int[] arr){
for(int i=0;i<arr.length-1;i++){
//这里,有一个比较巧妙的方法,就是for循环从数组的第0个元素开始,直到倒数第2个元素,每次都假定第i个元素是最小的元素,然后把这个最小元素的下标赋给一个变量来记录。
//每次循环的时候,都先假定这第i个元素是最小的,并把这个下标赋给minIndex.
int minIndex=i;
//接下来,就是要从第[i+1]开始到最后一个元素中,找出一个最小的元素,且该元素比minIndex还要小的那个元素。如果找到了的话,则把这2个元素交换位置。即:交换i和minIndex这2个元素。
for(int j = i+1;j < arr.length; j++){
if(arr[j] < arr[minIndex]){
//注意,这里找到的第j个元素不但比arr[minIndex]要小,而且它一定还是【i+1,arr.lengh】区间中最小的那个元素。如果找到了,则把我们原先假定的最小的那个元素,和这个真正的最小的元素交换位置。
minIndex = j;
}
}
swap(arr,i,minIndex);
}
}
//因为sort()是static的,所以这里的swap()也必须是static
private static void swap(int[] arr,int i;int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
//写一个main方法,对排序算法进行测试
public static void main(String[] args){
int[] arr={7,2,5,4,3,100};
SelectionSort.sort(arr);
for(int key:arr){
System.out.print(key+" ");
}
System.out.println();
Random random=new Random();
arr=new int[100];
for(int i=0;i<100;i++){
arr[i]=random.nextInt(1000);
}
SelectionSort.sort(arr);
for(int key:arr){
System.out.print(key+" ");
}
}
}4 “低效版”选择排序算法
public class SelectionSort{
private SelectionSort(){};
public static void sortSlow(int[] arr){
for(int i=0;i<arr.length-1;i++){
for(int j=i+1;j<arr.length;j++){
if(arr[j]<arr[i]){
swap(arr,i,j);
}
}
}
}
private static void swap(int[] arr,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
}对比这个“低效版”选择排序算法,可以看到,我们在从第[i+1,arr.length]区间中,每当有元素比arr[i]小的话,则立即交换它们的顺序,这样一来,如果后面还有更小的元素,则仍需要继续交换。
而前一种选择排序算法,则是先从第[i+1,arr.length]区间中找到该区间的最小元素,并记录下它的索引位置minIndex,最后再交换第i个和第minIndex个元素。显然,其性能会快很多,因为其需要交换元素的次数少了很多。这也正是一个好的算法的魅力所在。
5选择排序算法和“低效版”选择排序算法性能测试对比
完整的代码如下:
import java.util.Arrays;
import java.util.Random;
/**
* @Author:asher
* @Date:2021/3/4 19:52
* @Description:DataStructureAlgorithm.SelectionSort
* @Version:1.0
*/
public class SelectionSort {
private SelectionSort(){}
public static void sort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i+1; j <arr.length; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
swap(arr, i, minIndex);
}
}
public static void sortSlow(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = i+1; j <arr.length ; j++) {
if (arr[j] < arr[i]) {
swap(arr, i,j);
}
}
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
Random random = new Random();
int count=100000;
//初始化1个100000个元素的数组
int[] arr1 = new int[count];
for (int i = 0; i <count; i++) {
//实例化这个数组,每个元素都是随机生成,元素大小上限也为100000
arr1[i] = random.nextInt(count);
}
//copy这个数组,便于后续排序对比
int[] arr2 = Arrays.copyOf(arr1, arr1.length);
//选择排序算法测试
long t1=System.currentTimeMillis();
SelectionSort.sort(arr1);
long t2 = System.currentTimeMillis();
System.out.println("sort time ms:"+ (t2 - t1));
//"低效版"选择排序算法测试
long t3=System.currentTimeMillis();
SelectionSort.sortSlow(arr2);
long t4 = System.currentTimeMillis();
System.out.println("sortSlow time ms:"+ (t4 - t3));
}
}
//测试执行结果:
//sort time ms:4604
//sortSlow time ms:177106 带泛型的选择排序算法
前面的选择排序算法,只是针对整型数组的排序,但是其通用性还不强,接下来,我们动手把它改造为支持任意类型数组的选择排序算法,即带泛型的选择排序算法。
import java.util.Random;
public class SelectionSort{
private SelectionSort(){};
//这里只需要改为泛型方法即可,并不需要把类改为泛型类,因为该类被当做工具类来使用,并没涉及到带泛型的成员变量
//这里的参数中数组类型是带泛型T的,因此方法的返回值void前也需要指定泛型。
//同时T extends Comparable<T>,此处的extends意味着这个泛型类T是实现Comparable接口,而不是当做继承来理解
//此处要实现Comparable接口的原因是,arr[j]和arr[minIndex]此时被当做对象实例来比较,需要调用compareTo()方法,而不能再是使用小于<来比较大小了
public static <T extends Comparable<T>> void sort(T[] arr){
for(int i=0;i<arr.length-1;i++){
int minIndex=i;
for(int j=i+1;j<arr.length;j++){
//arr[j]和arr[minIndex]此时被当做对象实例来比较大小
if(arr[j].compareTo(arr[minIndex])<0){
minIndex=j;
}
}
swap(arr,i,minIndex);
}
}
private static <T> void swap(T[] arr,int i,int j){
T temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
public static void main(String[] args){
int count=100000;
Random random=new Random();
Integer[] arr=new Integer[count];
for(int i=0;i<count;i++){
arr[i]=random.nextInt(count);
}
long beginTime=System.currentTimeMillis();
SelectionSort.sort(arr);
long endTime=System.currentTimeMillis();
System.out.println("Generics Array selection sort time:"+(endTime-beginTime));
}
}
//输出结果:
//Generics Array selection sort time:13643这里,可以看到,同样的选择排序算法,同样的数据量10万个,对于基本类型的数组int[]排序耗时4604ms,而对于包装类型Integer[]排序耗时13643。差别还是比较明显的,原因在于包装类型的数据是放在heap内存区,被当做对象来比较,而基本类型的数据是直接放在stack内存区进行比较大小的。
7 对自定义类使用选择排序进行排序
我们对选择排序算法改造成了可以支持泛型的排序算法,即对任意数据类型的数据进行排序。我们自定义一个Student类,让其实现Comparable接口,在compareTo()方法中,先按身高排序,再按年龄进行排序。
public class Student implements Comparable<Student>{
private String name;
private int height;
private int age;
public Student(String name,int height,int age){
this.name=name;
this.height=height;
this.age=age;
}
@Override
public int compareTo(Student stu){
if(this.height!=stu.height){
return this.height-stu.height;
}else{
return this.age-stu.age;
}
}
@Override
public String toString(){
return "Student: name="+name+" height="+height+" age="+age;
}
}在SelectionSort的main方法中,对Student[]数组进行排序,代码片段如下:
public static void main(String[] args){
Student[] students={new Student("Jim",120,7),
new Student("Kate",120,7),
new Student("Tom",110,5)};
SelectionSort.sort(students);
for(Student stu:students){
System.out.println(stu);
}
}
//结果如下:
Student: name= Tom height=110 age=5
Student: name= kate height=120 age=7
Student: name= Jim height=120 age=7从上,可以看到,支持泛型的选择排序算法,可以对任意类型的数据进行排序了。同时,看到排序之后,Jim和Kate这2个学生对象的身高,年龄一致,且在原数据中,Jim排在前面,但是排序之后的结果却在后面。所以,验证了选择排序是不稳定的排序算法。
8 时间复杂度分析
public static <T extends Comparable<T>> void sort(T[] arr){
for(int i=0;i<arr.length-1;i++){
int minIndex=i;
for(int j=i+1;j<arr.length;j++){
//arr[j]和arr[minIndex]此时被当做对象实例来比较大小
if(arr[j].compareTo(arr[minIndex])<0){
minIndex=j;
}
}
swap(arr,i,minIndex);
}
}假定数组长度为n,当外循环i=0时,内循环执行n-1次,i=1时,内循环执行n-2次,,,直到i=n-1时,内循环执行0次。总计执行次数就是一个等差数列,首项是0,尾项是n-1,则其和为:n(0+n-1)/2=1/2(n2-n),而我们在评估时间复杂度时遵循的原则是去掉常数项、去掉低阶项,去掉系数项。所以,评估出的时间复杂度是O(n2)。同时,我们可以分别测试1万、10万个数据项的数组,执行选择排序,来看其执行时间是否大概差别100倍?如果后者执行耗时大概是前者的100倍的话,而数据量是前者的10倍,那么就可以证明该算法的复杂度是O(n2)。我在本地测试的结果不太准,同样的算法思路,不同的测试结果:
SelectionSort ,10000 ,0.134 s SelectionSort ,100000 ,13.731 s ----------------------------------------------------------- 10000 time: 0.082 100000 time: 12.608
9 小结
选择排序算法,见名知意,就是第1次从所有元素中选择一个最小的元素放在第1个位置处,第2次从剩下的元素中选择一个最小的放在第2个位置处,以此类推,直到最后1个元素。同时,我们可以说,对于第i次选择的时候,数组中从[0,i)的所有元素都已经是有序的,从[i,n)中的元素还都是无序的状态。